If you’re just starting out with machine learning or statistics, you might already know about linear regression, a method used to predict continuous outcomes based on input features. But real-world data is often tricky. When features are closely related or there are too many, linear regression may struggle to make reliable predictions. That’s where Ridge Regression comes into play.
In this article, we’ll explore what Ridge Regression is, why it’s important, how it works and when you should use it, all in straightforward language anyone can understand.

Why Do We Need Ridge Regression?
Imagine you want to predict the price of a house using different features like the size of the house, number of bedrooms, age, and location. Sometimes, some features can be strongly related to each other for example, the size of the house and the number of bedrooms often go hand-in-hand. This situation is called multicollinearity.
Multicollinearity can cause problems for simple linear regression because it makes the model unstable. The coefficients (weights assigned to each feature) can become very large or fluctuate wildly, which leads to poor predictions on new data. Additionally, when a model fits the training data too closely including noise , it’s called overfitting.
Ridge Regression helps solve these problems by adding a constraint that keeps the coefficients small and stable.
What Exactly is Ridge Regression?
Ridge Regression is a type of regularized linear regression. It builds on ordinary linear regression but adds a penalty on the size of the coefficients.
In regular linear regression, the goal is to find coefficients that minimize the total squared difference between the predicted values and the actual values. Ridge Regression changes the formula by adding a penalty proportional to the sum of the squares of the coefficients.
The Ridge Regression Formula
Let’s say:
- y is the actual outcome.
- y^ is the predicted outcome.
- βj are the coefficients (weights) of the features.
- λ (lambda) is a parameter that controls the penalty strength.
The Ridge Regression aims to minimize:
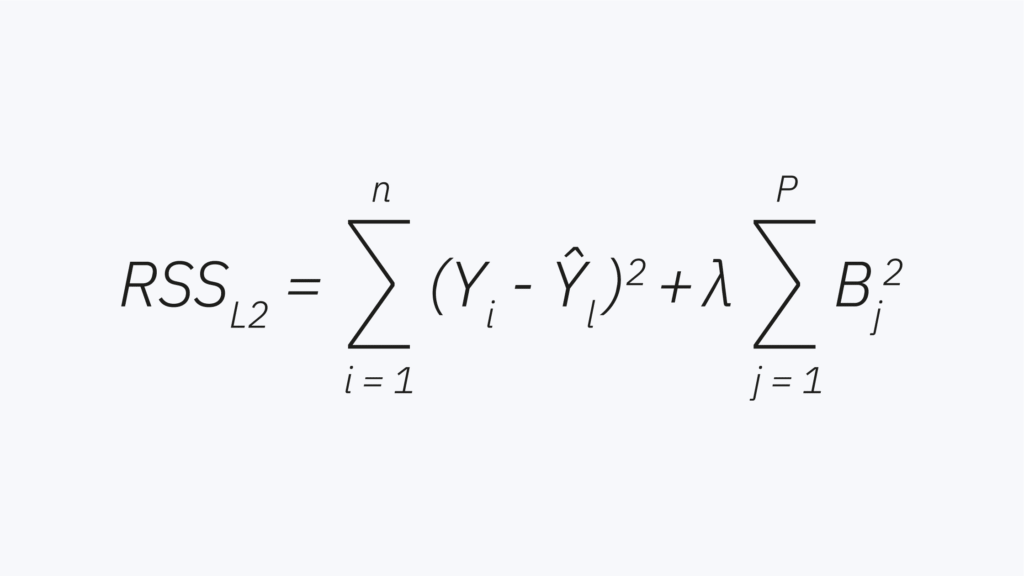
The first part measures how well the model fits the data and the second part discourages large coefficients.
What Does the Penalty Do?
By adding this penalty term, Ridge Regression shrinks the coefficients toward zero, but unlike some other methods, it doesn’t make them exactly zero. This shrinkage helps:
- Reduce the impact of noisy or irrelevant features.
- Prevent the model from relying too heavily on any single feature.
- Make the model more stable and generalizable on new data.
Choosing the Penalty Strength: The Lambda (λ) Parameter
The penalty’s strength is controlled by the regularization parameter λ\lambda:
- If λ = 0, Ridge Regression is just regular linear regression with no penalty.
- If λ is very large, coefficients shrink closer to zero and the model becomes simpler but might miss important patterns (underfitting).
- Usually λ is chosen carefully using methods like cross-validation which tests different values to find the best balance between fitting and generalization.
When Should You Use Ridge Regression?
Ridge Regression is particularly useful when:
- You have many features, and some of them are correlated.
- Your linear regression model is overfitting the training data.
- You want a model that is more stable and reliable for making predictions.
- You want to keep all features in the model but reduce their influence.
How is Ridge Regression Different from Lasso?
Both Ridge and Lasso Regression are regularization methods, but they differ in the penalty type:
- Ridge uses L2 regularization (sum of squared coefficients).
- Lasso uses L1 regularization (sum of absolute values of coefficients).
This means Lasso can shrink some coefficients exactly to zero, effectively performing feature selection by removing some features entirely. Ridge only reduces coefficients but keeps all features in the model.
Real-World Example: Predicting House Prices
Suppose you want to predict house prices but notice that some features, like square footage and number of rooms, are highly correlated. Ordinary linear regression might assign unstable, large weights to these features, causing unreliable predictions.
By applying Ridge Regression, you add a penalty to these large weights, making the model more stable. The resulting model might be slightly less precise on training data but will perform better on new, unseen houses.
Why Ridge Regression Matters ?
| Issue in Linear Regression | How Ridge Regression Helps |
|---|---|
| Multicollinearity | Shrinks correlated feature weights |
| Overfitting | Penalizes large coefficients |
| Model instability | Produces smoother, more stable models |
| Many correlated features | Keeps all features but controls impact |
Python Example
Here is how you can use Ridge Regression with Python’s scikit-learn library:
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
# Sample data: Features and target
X = np.array([[1, 2], [2, 4], [3, 6], [4, 8], [5, 10]])
y = np.array([3, 5, 7, 9, 11])
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Create Ridge Regression model with lambda = 1 (alpha in sklearn)
model = Ridge(alpha=1.0)
# Train the model
model.fit(X_train, y_train)
# Predict on test set
y_pred = model.predict(X_test)
# Calculate error
print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
Final Thoughts
Ridge Regression is a powerful extension of linear regression that helps you build more reliable models, especially when dealing with many correlated features or noisy data. By controlling the size of coefficients, it prevents overfitting and makes your model better at predicting new data.
Whether you’re working on academic projects or real-world applications, understanding Ridge Regression will add a valuable tool to your machine learning toolkit.


3 thoughts on “What is Ridge Regression?”