Simplifying the Mathematics of Neural Networks and Deep Learning

Neural networks are the foundation of modern artificial intelligence, powering everything from voice assistants to medical image analysis. While their results may seem almost magical, at the heart of these systems lies a precise, structured mathematical framework. Understanding this framework is not just an academic exercise, it’s the key to building better, faster, and more reliable AI models.

In this guide, we’ll break down the mathematics of neural networks and deep learning into digestible parts. From forward propagation to the universal approximation theorem, you’ll learn how each mathematical component contributes to making neural networks work and why mastering these concepts can give you a significant edge as an AI practitioner.

1. Forward Propagation: How Neural Networks Process Data

At their simplest, neural networks are sequences of mathematical operations applied layer by layer to input data. The process of generating predictions from inputs is called forward propagation.

Here’s how it works:

• Linear transformation: For each neuron, the network calculates a weighted sum of its inputs, plus a bias term: z=w1x1 + w2x2 +…+ wnxn + b
• Non-linear activation: Functions like ReLU, sigmoid, or tanh are applied to introduce non-linearity. Without this step, the network would behave like a simple linear regression, unable to capture complex relationships.

By stacking many layers, a network can represent highly complex mappings from inputs to outputs, making it ideal for image recognition, natural language processing, and more.

2. Loss Functions: Measuring Prediction Accuracy

A neural network needs a way to measure how well it’s performing. That’s where loss functions come in—they quantify the difference between the predicted output and the actual target.

Common choices include:

• Mean Squared Error (MSE): Ideal for regression tasks.
• Cross-Entropy Loss: Popular in classification problems because it penalizes confident but wrong predictions more heavily.

The loss value becomes the feedback signal for the learning process. A high loss means the network is far from correct, while a low loss indicates it’s closer to the target.

3. Backpropagation & Jacobians: Learning from Mistakes

To improve, a neural network needs to know how to adjust its weights. Backpropagation is the algorithm that makes this possible.

• It uses the chain rule of calculus to calculate gradients—partial derivatives of the loss function with respect to each weight.
• Jacobians extend this concept to handle vector-valued outputs, making computations efficient in deep architectures.

This process determines the exact “direction” in which each weight should move to reduce the loss.

4. Gradient Descent: Optimization in Action

Once we have gradients, we need a way to update the weights. That’s where gradient descent comes in:

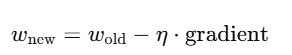
Here, η\eta is the learning rate. Setting it too high can cause the model to overshoot optimal values, while too low makes learning painfully slow.

Variants like stochastic gradient descent (SGD), Adam, and RMSProp are widely used in modern deep learning because they handle noisy, high-dimensional data well.

5. The Universal Approximation Theorem: Why Neural Networks Work

The Universal Approximation Theorem states that a neural network with at least one hidden layer and a non-linear activation can approximate any continuous function to arbitrary precision, given enough neurons.

This means that, in theory, neural networks are capable of modeling almost any relationship in data—whether it’s recognizing a face or predicting stock prices.

6. Advanced Optimization: Beyond Basic Gradient Descent

While gradient descent is the workhorse of training, advanced methods can improve convergence:

• Momentum-based optimization: Helps escape shallow minima by adding a fraction of the previous update to the current step.
• Quasi-Newton methods (e.g., BFGS): Use curvature information for more efficient updates.
• Conjugate Gradient & Levenberg–Marquardt: Effective for specific types of problems with complex error surfaces.

These methods help reduce training time and improve stability, especially in deep and complex networks.

7. The Complete Learning Cycle of a Neural Network

Training a neural network involves a repeating sequence:

1. Forward pass – Input data flows through the network to produce predictions.
2. Loss calculation – The difference between predictions and actual values is measured.
3. Backpropagation – Gradients are computed for each parameter.
4. Optimization step – Weights are updated based on the gradients.
5. Iteration – The process repeats until performance is satisfactory.

This cycle, combined with the network’s theoretical ability to approximate functions, is what makes deep learning both powerful and practical.

Why Understanding the Math Matters for AI Practitioners

Many practitioners rely on high-level frameworks like TensorFlow or PyTorch without fully understanding the math under the hood. But mastering these concepts allows you to:

• Troubleshoot problems like vanishing or exploding gradients.
• Choose the right architecture for your task.
• Fine-tune learning rates and other hyperparameters.
• Apply advanced training techniques with confidence.

In short, the math empowers you to go from “using” neural networks to truly engineering them.

Conclusion

The mathematics of neural networks forward propagation, loss functions, backpropagation, gradient descent, and the universal approximation theorem form the backbone of deep learning.

By understanding these principles, you can build more effective models, troubleshoot issues efficiently and innovate beyond pre-built architectures.

Deep learning might seem complex at first but when broken down into its mathematical components, it follows a logical, step-by-step process. Whether you’re a beginner aiming to grasp the essentials or a seasoned developer refining your models, the math is your most powerful tool for unlocking the full potential of neural networks.

Related Reads

• LLM Engineer Toolkit – Your Complete Map to 120+ LLM Libraries
• Prompt Engineering vs. Fine-Tuning: Choosing the Right Strategy for Optimizing LLMs in 2025
• MLOps in 2025: Best Practices for Deploying and Scaling Machine Learning Models
• GPT-5: The Unstoppable Next-Gen Revolution Redefining Artificial Intelligence
• DeepSeek: Top 2 Open-Source AI Model for Language, Code and Reasoning

External Resources

Deep Learning Book by Ian Goodfellow (Chapter on Mathematical Foundations)
https://www.deeplearningbook.org/

Neural Networks and Deep Learning (Free Online Book)
http://neuralnetworksanddeeplearning.com/

3Blue1Brown – Neural Networks (Visual Introduction to Mathematics Behind NN)
https://www.3blue1brown.com/topics/neural-networks

PyTorch Official Documentation
https://pytorch.org/docs/stable/index.html