Lasso Regression is one of the most powerful techniques in machine learning and statistics for regression analysis. It is especially useful when you have a large number of features and want to identify the most important ones.
Table of Contents
What is Regression?
Before diving into Lasso Regression, let’s briefly understand what regression means. In simple words, regression is a method used to predict a continuous outcome based on one or more input variables (also called features or predictors). For example, you might want to predict a person’s weight based on their height and age.
The most basic form of regression is Linear Regression which assumes a straight-line relationship between the input variables and the target variable.
Why Do We Need Regularization?
In real-world datasets, we often face challenges like:
- Too many features (high dimensionality)
- Overfitting (the model performs well on training data but poorly on new data)
- Multicollinearity (features are highly correlated)
To handle these problems, we use regularization techniques. Regularization adds a penalty term to the loss function (which the model tries to minimize), preventing the model from becoming too complex.
What is Lasso Regression?
Lasso Regression, short for Least Absolute Shrinkage and Selection Operator, is a regularized form of linear regression. It not only helps reduce overfitting but also performs feature selection meaning it automatically eliminates the least important features by shrinking their coefficients to zero.
Lasso Regression modifies the cost function of Linear Regression by adding a penalty term equal to the absolute value of the coefficients:
Lasso Regression Formula:
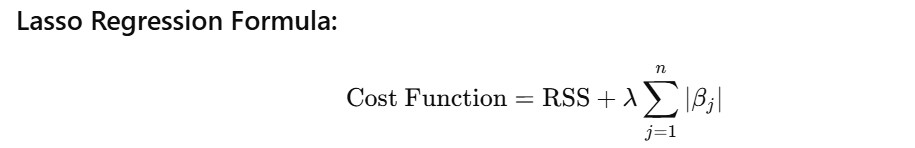
Where:
- RSS = Residual Sum of Squares (difference between predicted and actual values)
- βj = coefficient of the jth feature
- λ = regularization parameter (controls the strength of the penalty)
How Does Lasso Work?
The Lasso penalty term λ∑∣βj∣ encourages the model to shrink the less important feature coefficients toward zero. When λ is large enough, some of these coefficients become exactly zero, effectively removing those features from the model.
This makes Lasso Regression especially useful when you have a lot of features and suspect that many of them are not important.
Difference Between Lasso and Ridge Regression
Lasso Regression is often compared to another regularization technique called Ridge Regression. Here’s the difference:
| Aspect | Lasso Regression | Ridge Regression |
|---|---|---|
| Penalty Type | L1 penalty (absolute value) | L2 penalty (squared value) |
| Feature Selection | Yes (can shrink coefficients to zero) | No (shrinks but doesn’t eliminate) |
| Best for | Sparse models, feature elimination | Multicollinearity, regularization |
In practice, Lasso is used when you want a simpler model that automatically removes irrelevant features.
Advantages of Lasso Regression
- Feature Selection: Lasso automatically drops irrelevant variables, simplifying the model.
- Prevents Overfitting: By penalizing large coefficients, Lasso avoids overly complex models.
- Easy to Interpret: With fewer features, the model becomes more interpretable.
- Good for High-Dimensional Data: When the number of features is greater than the number of observations, Lasso performs well.
Disadvantages of Lasso Regression
- Instability with Correlated Features: Lasso might randomly select one feature among correlated ones, ignoring others.
- Bias in Coefficients: Lasso tends to shrink coefficients, which can lead to biased estimates.
- Not Ideal When All Features Matter: If all input variables are important, Ridge might be a better choice.
Choosing the Right Lambda (Regularization Parameter)
The performance of Lasso Regression largely depends on the value of λ\lambda. A higher value means more regularization (more coefficients shrink to zero) while a lower value means less regularization.
We usually select the best value of λ using cross-validation. Libraries like Scikit-learn in Python offer tools like LassoCV that automatically find the optimal lambda value.
When to Use Lasso Regression
You should consider using Lasso Regression when:
- You have a large number of features.
- You want to perform automatic feature selection.
- Your dataset has some irrelevant or less important variables.
- You are facing overfitting issues with standard linear regression.
Lasso Regression in Python
Here’s a simple code example using Scikit-learn:
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Load dataset
data = load_boston()
X = data.data
y = data.target
# Split into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Train Lasso Regression model
model = Lasso(alpha=1.0)
model.fit(X_train, y_train)
# Make predictions
y_pred = model.predict(X_test)
# Evaluate model
print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
print("Model Coefficients:", model.coef_)
Note: In real-world scenarios, consider standardizing your features using
StandardScalerbefore applying Lasso Regression.
Conclusion
Lasso Regression is a powerful tool in a data scientist’s toolkit. It not only helps improve model performance through regularization but also simplifies models by automatically selecting the most important features.
In an age where datasets are becoming increasingly complex and high-dimensional, understanding and using Lasso Regression can lead to more efficient, interpretable and accurate predictive models.
If you’re looking to boost your machine learning model performance, avoid overfitting or select the best features, Lasso Regression might be exactly what you need.

1 thought on “What is Lasso Regression?”